نویسنده: ماکس بورن/ مترجم: هوشنگ گرمان
1. منشاء اندازه گیری فضا و زمان
مسئله فیزیکی فضا و زمان مطلبی است ساده و بدون شاخ و برگ، تثبیت یک مکان و یک زمان مشخص است برای هر رویداد طبیعی و به منظور بازیافتنی کردن آن رویداد از درون هرج و مرج همجواری و توالی چیزها.
نخستین تکلیف انسان، آشنا شدن با محل خویش در سطح زمین بود. از این جا فن مساحی زمین سرچشمه آموزش فضا گردید، و واژه «ژئومتری = زمین سنجی» (هندسه) هم از همین چشمه تراوش کرد. ولی مقیاس سنجش زمان ابتدا از توالی شب و روز، تغییر اهله ماه و تبدیل فصلهای سال به دست آمد. این پدیده های چشمگیر آدمی را نخست بر آن داشت که به آسمان و ستارگان بنگرد، علم کاینات از همین جا آغاز شد. علم نجوم معلومات آزموده شد بر سطح زمین را به فضاهای آسمان، به دوریهای معین و به مدار ستارگان انتقال داد. انسان به منظور تمیز بین گذشته و اکنون و آینده و تعیین جایی بر حسب زمان برای هر چیز، معیاری از آسمان کسب کرد.
2. یکای طول و زمان
تثبیت یکای اندازه گیری، پایه هر نوع سنجش فضا و زمان است. اعلام «طولی به چند متر»، به معنای نسبت طول مزبور است به طول یک متر. همچنان اعلام «زمانی به چند ثانیه»، به معنای نسبت زمان مزبور است به مدت زمان یک ثانیه. پس مسئله همیشه بر سر نسبت بین اعداد دور می زند، یعنی بیان اندازه های نسبی بر حسب یکاهای سنجش. اما این یکاها، با توجه به پاره ای ویژگیها، مانند قابلیت تجدید و تکثیر یا انتقال پذیری و درجه استحکام و مدت دوام، تا یک حد نسبتاً وسیع آزادنه و اختیاری انتخاب می شوند.
یکای طول در فیزیک سانتی متر(cm) است، و آن طول یکی از صد قسمت متساوی متر نمونه ای است که در پاریس محافظت می شود (1). اگرچه این متر نمونه در اصل بایستی یک نسبت دقیقاً صحیح با محیط دایره عظیمه داشته باشد، یعنی طول آن درست به اندازه یک میلیونیوم ربع دایره مزبور باشد، ولی از آزمایشهای جدید برمی آید که نسبت این دو طول تا این حد دقیق نیست.
یکای زمان در فیزیک ثانیه (sec) است و نسبت آن به زمان یک دور گردش زمین و مشخص است. اکنون مسلم شده است که تعریف یکاها بر حسب محیط و زمان گردش زمین، چندان کاربردی ندارد. از این رو امروزه یکاها با استفاده از خصوصیات اتمی ماده به صورتی انتخاب می کنند که عمل بازسازی آنها آسانتر باشد. پس تعریف سانتی متر چنین خواهد شد که بیان شود، این یکا چند طول موج یک اشعه معین الکترومغناطیسی را که از اتم کادمیوم صادر می شود، در بر می گیرد. ثانیه هم به همین نحو می تواند به صورت مضرب صحیح دوره نوسان مولکول یک عنصر مشخص تعریف شود.
3. نقطه صفر و دستگاه مختصات
اگر علاوه بر طول و مدت، مکان و لحظه وقوع رویدادی را نیز بخواهند تعیین کنند، به معلومات قبلی بیشتری نیاز دارند. در مورد زمان که به تصور ما تکبعدی می نماید، تثبیت یک نقطه صفر کافی است. مورخان ما میلاد مسیح را به عنوان این نقطه صفر برای محاسبه سالها تعیین کرده اند. ولی اخترشناسان، بنا بر هدفی که از آزمایشهای خود دارند، از دیگر نقطه های صفر موسوم به دورانها استفاده می کنند. چنانچه یکا و نقطه صفر تثبیت شده باشد، هر رویدادی را به وسیله اعلام یک عدد می توان مشخص کرد.
در هندسه، به معنای محدود آن که تعیین مکان در سطح زمین است، برای تعیین هر مکانی دو اطلاع باید در دست باشد. مثلاً «خانه من در فلان خیابان واقع شده است» برای یافتن خانه کافی نیست، شماره خانه را نیز باید بر این نشانی افزود. در بسیاری از شهرهای آمریکا حتی خیابانها هم شماره دارند. مثلاً «خیابان 13، شماره 25» که دو شماره را اعلام می کند، یک نشانی کامل است. و این در واقع همان سبک نشانه گذاریی است که در نزد ریاضیدانان «تعیین مختصات» خوانده می شود.
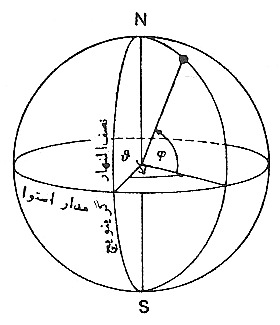ش. 1- θ و φ به ترتیب طول و عرض جغرافیائی یک نقطه P واقع بر سطح زمین. θ از نصف النهار گرینویچ، و φ از مدار استوا محاسبه شده است. N قطب شمال، S قطب جنوب.
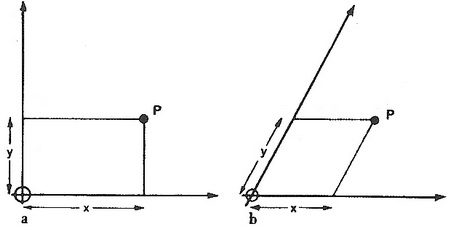ش. 2- نمایش یک نقطه واقع بر یک سطح با تصاویر آن بر دو محور مختصات x و y ؛2a در دستگاه مختصات قائم، 2d در دستگاه مختصات مایل.
جغرافیدانان عموماً از طول و عرض جغرافیایی استفاده می کنند. (ش.1)، برای طولها از نصف النهار گرینیچ به سمت شرق، برای عرضها از مدار استوا به دو سمت شمالی جنوبی، در این قسم نشانه گذاری، نقاط صفر هم در ضمن تثبیت می شوند، به این صورت که نصف النهار گرینیچ به عنوان نقطه صفر طولها، و خط استوا به عنوان نقطه صفر عرضها. در بررسیهای هندسه مسطحه معمول این است که از مختصات قائم استفاده می کنند (ش. 2a) و x و y در این شکل فاصله نقطه p از دو محور متعامد را نمایش می دهند. همچنین گاهی پیش می آید که از دیگر انواع مختصات استفاده می کنند، مثلاً از مختصات مایل (ش. 2b) یا از مختصات قطبی (ش.3).اگر دستگاه مختصات از قبل معین شده باشد، جای هر نقطه از سطح مختصات را به وسیله دو عدد می توان نمایش داد.
تعیین مکان در فضا نیز به همین صورت است، منتهی در این جا شناسایی سه مختصات لازم است، و باز ساده تر از این خواهد بود که از سه محور متعامد z، y، x استفاده می شود (ش.4).
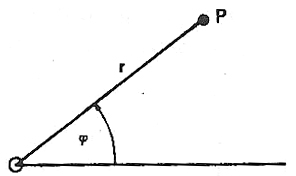ش.3- نقطه p با مختصات قطبی r و φ بر سطح. شعاع r فاصله ی نقطه ی p از مبدأ مختصاترا نشان می دهد و φ زاویه انحراف شعاع r از خط مبدأ را.
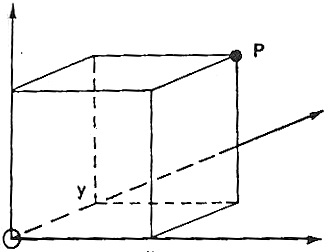ش.4- نمایش نقطه ی p در فضا به وسیله ی سه برش محوری x، y و z در دستگاه مختصات قائم.
4. اصلهای متعارف هندسی
هندسه باستان، به عنوان علم، توجه خود را کمتر به تعیین مکان بر سطح معطوف داشته و بیشتر به شکل و اندازه قطعات مسطح و فضایی و همچنین به قوانین مربوط به این شکلها پرداخته است. ریشه این امر را باید در فن مساحی و هنر معماری جست، زیرا که هندسه نیازهای خود را بدون استفاده از مفهوم مختصات نیز مستقلاً برطرف می کرده است.
اصلهای هندسه مقدم بر همه به چیزهایی اکه خود آنها را نقطه و خط و سطح می نامد، صفاتی نسبت می دهد. این چیزها در قوانین هندسه سنتی یونان، در مصنفات اقلیدس (2) (300 سال ق م)، تعریف نمی شوند و فقط به ذکر نام و شرح صفاتشان اکتفا می گردد. به این ترتیب، وظیفه شناسایی این چیزها به قوه تصور واگذار شده است، و کسی که می خواهد به هندسه بپردازد، باید از قبل بداند که مثلاً خط راست چیست. یال دیوارخانه ای یا لبه تیز دراز سنجی را در عالم تجرید و جدا از هر ماده به تصور آورده وجود خط مستقیم را بدین نحو تصدیق می کنند، آنگاه چند عبارت معدود که ارتباط منطقی این صورتهای انتزاعی را باید بیان کند، ارائه می دهند. اما شاهکار یونانیان درست در کشف همین چند عبارت است، زیرا که اگر همین چند عبارت معدود در حکم بدیهیات پذیرفته شوند، دیگر عبارتهای این علم صحت خود را به حکم منطق و جبر تحمیل خواهند کرد. این چند عبارت مقدماتی را «اصلهای متعارف» می نامند. این اصلها از طریق استدلال و برهان قابل اثبات نیستند، ریشه های منطقی هم ندارند، و منبع شناخت آنها را باید در جایی دیگر جستجو کرد. دراین باب که ریشه این اصلها در کجا قرار گرفته و چگونه است، بسیاری از فیلسوفان در طی قرنهای متمادی نظریه های متفاوت ارائه کرده اند. اما هندسه علمی این اصلها را خود تا پایان قرن هجدهم در حکم بدیهیات پذیرفت و دستگاه هندسی محض و صرفاً استدلالی را در قالب قضیه های هندسی بر پایه همین اصلها استوار ساخت.
در این جا نمی توانیم مسیر خودمان را عوض کنیم و معنای این صورتهای بسیط و چگونگی ریشه های شناخت این اصلهای متعارف را به تفصیل بیان می کنیم، اما خود را در موضعی قرار می دهیم که در مورد این مفهوم ها روشنی کامل وجود داشته باشد. پس فعلاً درست مانند بسیاری از نسلهای گذشته که این مفهومها را بدون کوچکترین ایهام و تردیدی به کار می برده اند، ما نیز آنها را بدان سان که در مدرسه آموخته ایم - یا دست کم می بایست بیاموزیم - همچنان به کار خواهیم برد. وضوح قضیه های متعدد هندسی و فواید علمی و رهنمودهایی که رویهم این دستگاه برای توجیه جهان و واقعیتها داشته است، می تواند به عنوان یک گواه کافی هرگونه شک و تردیدی را برطرف نماید.
5. منظومه عالم بطلمیوسی
آسمان مانند گنبدی کم و بیش تخت، آنچنان که بر آن ستارگان نصب شده باشند، به چشم می خورد. اما سراسر این گنبد گرد محوری که جای آن در آسمان به نشانه ستاره قطعی معین است، هر شبانه روز یک دور می چرخد. تا زمانی که این نمایش ظاهری در حکم یک پدیده واقعی می نمود، انتقال هندسه از زمین به مکانهای آسمانی زاید می بود و چنین انتقالی صورت نگرفت؛ چون دوریها و درازیهایی که در آن جاها یافت می شوند، در اندازه های زمینی نمی گنجند. به منظور نشانه گذاری موضع ستارگان کافی است که دو زاویه ظاهری را بشناسند، یکی زاویه ای که از شعاع دید ناظر به سمت ستاره با سطح افق پدید می آید، دوم زاویه ای که همین شعاع دید با سطحی دیگر که مناسب انتخاب شده باشد تشکیل می دهد. سطح زمین در این مرحله شناخت پست ترین طبقات را تشکیل می دهد و در قعر عالم قرار می گیرد. «بالا» و «پایین» به معنای مطلق کلمه به کار برده می شوند، و هر گاه در تخیلات شاعرانه یا در مکالمات فلسفی به «بلندی ثریا» و «پستی ثرا» اشاره شود، حاجت به توضیح اضافی نیست، زیرا که تجربه روزمره خود مستقیماً منظور را می رساند. مفهومهای علوم طبیعی در این مرحله هنوز همگی از درون معلومات ذهنی شکل می گیرند، و صورت عالم منتسب به بطلمیوس (3) (1500 سال ب. م.) در حقیقت بیان علمی همین مرحله فکری است. اما این فکر تا همین مرحله نیز به بسیاری از نکته های باریک حرکت خورشید و ماه و سیارات پی برده و با دستاوردهای ارزنده خود بر جنبه های نظری مسئله مسلط شده است، اگر چه بر سر اعتقاد دیرین خود همچنان سخت ایستاده است و زمین را ساکن مطلق و ستارگان را در دوریهای ناسنجیدنی به گرد زمین در حال گردش می پندارد. مدرا ستارگان بر پایه قوانین هندسه زمینی به صورت دایره های زمین مرکز و دایره های برون مرکز (4) تعیین می شوند، ولی این نه بدان معناست که فضای عالم تحت سیطره هندسه زمینی درآمده باشد، زیرا که مدارها مانند شیارهای پهن بر لایه های بلورین و منطبق که در مجموع آسمان خوانده می شود، سخت چسبیده اند.
6. منظومه عالم کوپرنیکی
می دانیم که متفکران یونانی شکل کروی زمین را از قبل شناخته بودند و پس از گذشتن از منظومه عالم زمین مرکزی بطلمیوسی، نخستین بار به بلندترین مدارج تجرید بدون پروا گام نهادند (آریستاخوس مقارن سال 300 ق م). اما از افول تمدن یونان نخست مدتها گذشته بود که کرویت زمین در دیگر سرزمینها و در نزد دیگر قومها واقعیت فیزیکی یافت. این نخستین روی گردانی شدید از صورت ظاهر بود و درعین حال نسخیتن روی آوری جدی به نسبی انگاری. از سر این نقطه عطف هم باز قرنها گذشت و آنچه که در آن روزگار کشفی بزرگ می نمود، برای خردسالان امروزی در شمار آموزشهای دبستانی شد. از این رو اکنون دشوار می توان به تصور آورد که نفی کردن معنای مطلق کلمه های «بالا» و «پایین» و پذیرفتن «متقاطرها» (5) به جای این دو اصطلاح، تا چه حد بر متفکران آن عصر گران می آمد و چقدر دشوار بود که اینان جهتی را که خود قبلا«پایین» می خواندند، از این پس «بالا» بخوانند. اما مسئله پس از تحقق یافتن مسافرت با کشتی به دور زمین، به اندازه ای روشن و آشکار می نمود که جای هیچگونه ابهام و تردیدی باقی نمی گذاشت. و به همین سبب نیز کشف کرویت زمین در اصل موجب نزاع و کشمکش بین دو جهان بینی عینی و ذهنی (پژوهشهای طبیعی و مکتب کلیسایی) نشد. این درگیری نخست زمانی روی داد که کوپرنیک (6)، (1543) مقام مرکزیت عالم را از زمین گرفت و منظومه عالم خورشید مرکزی را مطرح ساخت.
در این جا دشوار می توان گفت که نوعی نسبی انگاری پیشرفته تر عاید شده باشد، ولی اهمیتی که این کشف برای تحول فکر انسان داشته این بوده است که زمین (در نهایت انسان) از تخت یگانه «من» فرود می آید. زمین ماهواره خورشید می شود و انسانهای جنبنده اش را به دوش گرفته در فضای عالم گردش می دهد. دیگر سیاره هایی نیز همانند و هم ارز زمین بر مدارهای خود گردش می کنند: انسان از این پس دیگر از دیدگاه اخترشناسی مهم نیست. اما فراتر آنکه همه این تصورات خلاف عادی از آزمایشهای بزرگ و ستبر، از قبیل مسافرت با کشتی بادی به دور زمین، تراوش نمی کنند، بلکه از ترصدهایی جاری می شوند که برای آن روزگار بسیار دقیق و ظریف بوده اند، همچنین از یک رشته محاسبات بس پیچیده و دشوار حرکت سیارات؛ در هر حال از انبوهی اسناد و مدارکی که نه در دسترس همگان قرار می گیرد و نه برای زندگانی عادی روزانه مهم است. ظواهر، معتقدات، نوشته های بازمانده مذهبی و غیر مذهبی، همه یکسره خلاف آموزش نو حکم می کنند. اموزش نو یک کره غول پیکر برون از تصور آتشین را به جای قرص مرئی خورشید قرار می دهد و جای ستارگان خندان در آسمان در دوریهای برون از تصور به کره هایی می سپارد که خود همچنین آتشینند یا از نوع زمین غیر آتشین که نور بیگانه را باز می تابانند. در نهایت اینکه همه اندازه های مرئی می باید متشبه محسوب شوند، ولی فاصله های برون از تصور و سرعتهای برق آسا، حقیقت. با این وصف، آموزش نو می بایست فیروز شود، زیرا که توانایی این آموزش در اراده استوار هر انسان متفکری نهفته بود که می خواسته به توسط مفهومهای ساده و روشن، اگر هم این مفهومها صرفاً انتزاعی بوده، کلیه چیزهای جهان طبیعی را، حتی چیزی که برای هستی انسان هنوز ارزشی نداشته، تحت قانونمندی واحد قابل فهم کند. در این تحول که برای پژوهشهای علوم طبیعی بسیار مهم بوده است، اندیشه پروا ندارد که محسوسترین مشهودات را به دیده تردید بنگرد یا آن را از ریشه و بن نادرست بخواند، ولی در عین حال از خود تا بلندترین مدارج تجرید گام برمی دارد، تا واقعیت مورد اعتمادش را در آن جا از صورت طبیعت قرائت کند.
همه گامهای مشابه بیشمار ولی جزئی که در جهت نسبی انگاری علوم طبیعی در حال رشد برداشته می شوند، از اقدام بزرگ کوپرنیک سرچشمه می گیرند، تا نوبت به اینشتین می رسد و کار او با احترام تمام در ردیف سرمشقهای طلایی قرار می گیرد.
حال کیهان را، به گونه ای که کوپرنیک ترسیم کرده است، می باید در این جا شرح بدهیم.
نخست باید گفت که، مفهومها و قانونهای هندسه زمینی بدون مانع به مکانهای آسمانی مننتقل می شوند. جای دایره های نواری شکل عریض و تصوری جهانی بطلمیوسی را مدارهای واقعی دارای سطوح مداری متفاوت در فضا اشغال می کنند. خورشید در مرکز منظومه واقع می شود، و سیارات گرد خورشید روی مدارهای خود گردش می کنند. زمین از جمله این سیارات است و در عین گردش خودمحوری، مرکزی است برای مدار دایره ای ماه. علاوه بر این، خارج از منظومه ما ثوابتی نیز در مکانهای بینهایت دور هستند که مانند خوریشید ما در فضای عالم سا کنند. عمل سازنده کوپرنیک سندی است که به شرط پذیرفتن آن، صورت آسمان کلیه پدیده هایی را که در طرح سنتی منظومه عالم فقط با کمک فرضیه های ساختگی قابل توجیه بوده اند، بایستی به وضوح نمایان کند. در واقع هم همین طور است، چه اینک تبدیل شب و روز، تغییر فصلهای سال، پدیده اهله ماه، مدارهای حلقوی سیارات، همه به یکبار روشن و قابل فهم شده تحت محاسباتی نسبتاً ساده در می آیند.
7. تکمیل آموزش کوپرنیکی
چندان نگذشت که شکل مدارهای کوپرنیکی از آن پس دیگر با حاصل رصدها تطبیق نکرد. شکل این مدارها محققاً پیچیده تر از آن بوده است که به تصور می آمده. اینک برای اعتبار آموزش نو بسیار اهمیت داشت که، آیا به منظومه عالم بطلمیوسی برگردند، یا محاسبات نجومی را به راههای ساده بهتر کنند. ارزش جاودانی عمل کپلر (7) (1618) در این جاست که قوانین ساده و روشن سیارات را کشف کرد و بدین وسیله منظومه عالم کوپرنیکی را از بحران نجات داد. مدارها در حقیقت دایره های محیط بر خورشید نیستند، بکله منحنیهای بیضوی نزدیک دایره را مجسم می کنند که خورشید را در یکی از دو کانون خود جا داده اند. همچنانکه این قانون شکل مدارها را به نحوی ساده تنظیم می کند، قانون دوم و سوم کپلر به ترتیب سرعتی را که مدار به توسط سیاره پیموده می شود و ارتباطی را که بین زمان تناوب سیاره و بیضی مربوطه وجود دارد، به دست می دهند.
گالیله، هم عصر کپلر، دوربینی را که خود تازه اختراع کرده بود (1610) به سمت ستارگان متوجه ساخت و اقمار مشتری (8) را در ضمن این ترصدها کشف کرد. او در میان به صورت کوچک شده دستگاه سیارات برخورد و منظره تصوری کوپرنیک را به چشم خویش مشاهده نمود با این وصف، ارزش کارهای گالیله بیشتر در تحولی بوده است که وی به اصلهای مکانیک بخشیده بود، تا جایی که نیوتن (9) (1687) بعدها همین اصلهای تحول یافته را در مدارهای سیارات به کار بست و طرح منظومه عالم کوپرنیکی را تکمیل کرد.
دایره های کوپرنیکی و بیضیهای کپلری عبارتند از آنچه که به زبان دانش امروزی نمایش سینماتیکی یا فورنوماتیکی (10) مسیر حرکت (حرکت شناسی) نامیده می شود و وظیفه اش بیان ریاضی حرکت است، بدون آنکه به علل و ارتباطات دخیل در پیدایش حرکت اشاره کند. اما تعبیر علی قوانین حرکت را محتوای آموزشی تشکیل می دهد که علم دینامیک یا سینتیک (پویایی شناسی) خوانده می شود. نیوتن با به کار بستن دینامیک در حرکت جسمهای آسمانی، به تحلیل قوانین کپلر پرداخت و نیروی مکانیک را به طرزی داهیانه به عنوان علت حرکت وارد علم نجوم کرد. قانون جاذبه عمومی نیوتن با توضیحاتی که در خصوص همه بیقاعدگیهای قوانین کپلر می داده (منظور آنچه را که اختلالهای مداری خوانده می شد و در آن فاصله به علت دقیقتر شدن فن ترصدها مسئله حاد روز شده بود توجیه می کرده است) برتری خود را نسبت به نظریه های پیشین به اثبات رسانید.