نام: رویا بهشتی زواره (Roya Beheshti Zavareh)
تولد: 1977 - اصفهان - ایران
ملیت: ایرانی
دکترای دانشگاه ام آی تی، ورودی ۱۳۷۴ ریاضی دانشگاه صنعتی شریف
شهرت: ریاضیات، هندسه جبری
نشانی صفحه رسمی: http://www.math.wustl.edu/~beheshti
رویا بهشتی زواره، متولد ۱۳۵۶ در اصفهان است. رؤیا، در المپیاد سال ۱۹۹۴ هنگ کنگ در حالیکه فقط ۱۷ سال داشت، همراه با دیگر همراهانش افتخار آفریدند. او موفق شد در این دوره، مدال برنز را کسب نماید. اسامی دانش آموزان تیم ایران در سی و پنجمین المپیاد جهانی ریاضی به شرح زیر بود:
مازیار رامین راد، مریم میرزاخانی (مدال طلا)، رضا صادقی، رویا بهشتی زواره (مدال نقره)، علی نور محمدی و امید نقشینن (مدال برنز)
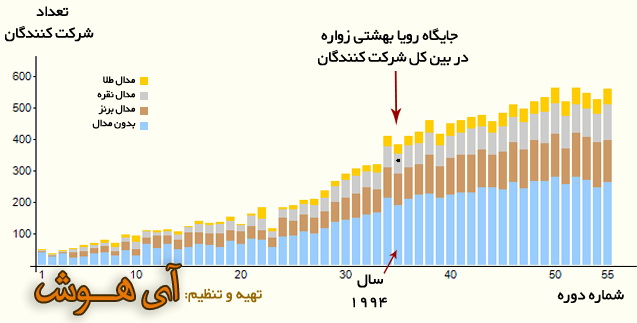
«مریم» و «رؤیا» از زبان مدیر دبیرستان فرزانگان:
خیریهبیگم حائریزاده، مدیر پیشین مجتمع آموزشی فرزانگان در مورد او و دست صمیمی اش مریم میرزاخانی چنین می گوید:
"اینجانب بهمدت هفتسال، مدیر دوره دبیرستان پروفسور «مریم میرزاخانی» و دکتر «رویا بهشتی» بودهام و نیز بهمدت ۳۴سال، مدیریت مجتمع آموزشی «موسسه منظومه خرد» را بر عهده داشتم، مایلم چندعامل مهم در موفقیت این دوعضو برجسته جامعه علمی جهانی را با نسل جوان دانشآموزان در هرکجا دنیا که هستند، مطرح کنم.
«مریم» و «رویا» هر دو در عمل نشان دادند که باور دارند معلم، یک راهنما و تسهیلکننده است و این خودشان هستند که باید یاد بگیرند. آنها بهخوبی یاد گرفته بودند که چگونه یاد بگیرند و تواناییهایشان را باور داشتند. «مریم» و «رویا» بهصورت یکتیم واقعی با هم کار میکردند. سینرژی حاصل از این کار تیمی بسیار بالا بود. علاوه بر هوش سرشار و پشتکار، تواضع ویژگی ممتاز «مریم» و اعتمادبهنفس بالا، ویژگی ممتاز رویا بود. کار تیمی این دونفر باعث میشد که ویژگیهای ممتازشان آنان را بهپیش ببرد.
«مریم» و «رویا» هرگاه که اراده میکردند کاری را انجام دهند، با پشتکار بالایی در آن کار موفق میشدند. آنها همواره از امکاناتی که در اختیار همه دوستانشان هم بود، بهخوبی استفاده میکردند. در موقعیتهای فرامدرسهای، مانند دانشجو رفتار میکردند، نه یکشاگرد مدرسه. هوش بالا، پشتکار، تواضع، اعتمادبهنفس، استفاده بهینه از امکانات موجود و کار تیمی از عوامل اساسی موفقیتشان بود. "
رویا بهشتی در ماه می ۲۰۰۳ دکترایش را از دانشگاه ام آی تی (MIT) زیر نظر پروفسور یوهان یانگ1 دریافت نمود. او در حال حاضر دانشیار2 ریاضی در دانشگاه واشنگتن در سنت لوئیس3 می باشد. حوزه تحقیقاتش، هندسه جبری4 می باشد. تحقیق او توسط بنیاد ملی علوم5 (NSF) حمایت شده است. (DMS1204567)
هندسه جبری شاخهای از ریاضیات است که مفاهیم جبر مجرد، به ویژه جبر جابجایی، را با مسائل هندسه میآمیزد. این شاخه از ریاضیات مدرن با آنالیز مختلط، توپولوژی و نظریه اعداد در ارتباط تنگاتنگ است. واریته مستوی (آفین) n-بعدی که یکی از بنیادی ترین مفاهیم این شاخه از ریاضی است دقیقا صفرهای مشترک تعدادی دلخواه از چند جمله ای های n-متغیره روی میدان مفروض تعریف می شود. بنابراین حلقه ی چند جمله ای ها نقش عمده ای در هندسه جبری ایفا می کند. تاریخ این علم گسترش فروانی دارد، طوری که قسمتی از مطالعات ارشمیدس مسائلی پیرامون مقاطع مخروطی، تشکیل می داد. همچنین ابن هیثم، فیزیکدان ایرانی قرن ۱۰ میلادی برای محاسبه ی مسافت ها مجبور به استفاده از معادلات درجه ی سوم می شده است. و نهایت اینکه خیام معادله ی درجه ی سوم را در کلی ترین حالت حل نمود. وی این کار را از طریق مقاطع مخروطی، و قطع دادن دایره با سهمی درجه دوم، انجام داد.
دیوید مامفورد6، پرفسور بازنشسته ریاضیات کاربردی در دانشگاه «براون» هندسه جبری را چنین توصیف می کند:
"هندسه جبری این شهرت را دارد که رشته ایست پیچیده، محرمانه و بسیار مجرد که طرفدارانش به طور سری در حال نقشه ریزی برای تصرف بقیه ریاضیات هستند و به نوعی این نکته آخر، درست است!"
تحصیلات:
1999: فارغ التحصیل دانشگاه صنعتی شریف (۲۲ سالگی)
2003: دریافت دکترا از دانشگاه MIT آمریکا. (۲۶ سالگی)
2003: پژوهشگر ارشد ریاضی، موسسه ریاضیات ماکس پلانک، آلمان (۲۶ سالگی)
2004: فوق دکترا، عضو ارشد پژوهشی دانشگاه کویین، کینگستون کانادا (۲۷ سالگی)
2006: فوق دکترای ریاضی عضو ارشد پژوهشی دانشگاه کالیفرنیا، برکلی آمریکا (۲۹ سالگی)
2006: استادیار ریاضی دانشگاه واشنگتن در سنت لوئیس آمریکا (۲۹ ساگی)
2009: دانشیار ریاضی دانشگاه واشنگتن در سنت لوئیس آمریکا (۳۲ ساگی)
اولین تألیف رسمی:
رویا بهشتی به همراه دوست صمیمی اش، مریم میرزاخانی، کتابی جهت آمادگی برای المپیاد ریاضی با عنوان نظریه اعداد، تألیف و منتشر نمودند. جزئیات بیشتری از این کتاب:
نام کتاب: نظریهٔ اعداد، از مجموعه کتابهای آمادگی برای المپیاد ریاضی
عنوان لاتین: Elementary Number Theory, Challenging Problems
تألیف: رؤیا بهشتی زواره، مریم میرزاخانی
ویرایش: ارشک حمیدی
چاپ هشتم - ۱۳۹۱
تعداد صفحات: ۳۰۴
شابک سیزده رقمی: ۹۷۸-۹۶۴-۳۱۸-۲۸۷-۸
شابک ده رقمی: ۹۶۴-۳۱۸-۲۸۷-۸
قطع کتاب: وزیری
وزن کتاب: ۴۲۴ گرم
پیشگفتار کتاب نظریهٔ اعداد
نظریهٔ مقدماتی اعداد چه از نظر مطلب و چه از نظر تنوع مسألههای مربوط به آن از زیباترین بخشهای ریاضیات مقدماتی است، و ویژگی بارز آن وجود مسألههایی است که گرچه بیانی ساده و مقدماتی دارند، اما یا حلنشده باقی ماندهاند و یا حل آنها نیاز به استفاده از ریاضیات پیشرفته دارد. در این کتاب به آموزش این بخش جذاب از ریاضیات مقدماتی پرداختهایم، بهگونهای که برای دانشآموزان علاقهمند دورهٔ دبیرستان مفید و قابل استفاده باشد. البته آنچه در این کتاب آمده بیشتر از آن مطالبی است که به زعم مؤلفان، دانشآموزان علاقهمند به شرکت در المپیادهای ریاضی باید بدانند، و برای این دسته از دانشآموزان مطالعهٔ فصلهای ۱ تا ۶ و فصلهای ۱۴ تا ۲۰ کافی است. برای مطالعهٔ این کتاب پیشنیاز خاصی بجز آشنایی با ابزارهای اساسی ریاضیات مقدماتی مانند اصل استقرای ریاضی و اصل لانهکبوتری لازم نیست.
فصلهای ۱ تا ۶ اساس فصلهای دیگرند، و برای مطالعهٔ بقیهٔ فصلها خواننده باید به مطالب آنها مسلط باشد. بهتر است فصلهای ۷ تا ۱۲ را دنبال هم خواند. در فصل ۱۱ قانون تقابل درجهٔ دوم را بیان و ثابت کردهایم. این قانون از مهمترین قضیههای نظریهٔ اعداد است و منشأ پیشرفتهای بسیاری در نظریهٔ اعداد بوده است. فصلهای ۱۴ تا ۲۱ همگی به بررسی جوابهای معادلات دیوفانتی اختصاص دارند. در این فصلها گاه از مطالب فصلهای ۷ تا ۱۳ استفاده کردهایم؛ خوانندهای که این مطالب را نخوانده است، میتواند از مطالعهٔ برهان قضیهها یا راهحل مسألههای مربوط صرفنظر کند. هدفمان از آوردن فصلهای ۲۵ و ۲۶ آشنا کردن خواننده با برخی شباهتها میان ویژگیهای اعداد صحیح و ویژگیهای چند جملهایهایی است که ضرایبشان اعدادی گویا هستند. هر چند این فصلها در انتهای کتاب آمدهاند، اما میتوان آنها را بعد از مطالعهٔ فصلهای ۱ تا ۶ خواند. در این کتاب تعداد زیادی مسأله آمده است. برخی از این مسألهها را کامل حل کردهایم. مسألههایی که بهعنوان تمرین در انتهای فصلها آمدهاند، اغلب سادهاند و برای تسلط یافتن بر مطالب هر فصل حل کردن آنها مفید است. مسألههایی که بهعنوان تمرینهای تکمیلی آمدهاند، دشوارترند، و بعضاً از میان مسألههایی انتخاب شدهاند که در المپیادهای مختلف مطرح یا پیشنهاد شدهاند.
آقای دکتر یحیی تابش مشوق ما در نگارش این کتاب بودهاند. از ایشان برای راهنماییها و نظرات مفیدشان تشکر میکنیم. همچنین از آقای ارشک حمیدی، ویراستار کتاب، برای پیشنهادات ارزشمند و زحمات فراوانشان در ویرایش این کتاب سپاسگزاریم.
رؤیا بهشتی زواره - مریم میرزاخانی -- شهریور ۷۸