بیوگرافی بزرگان ریاضی: حكیم عمر خیام
غیاثالدین ابوالفتح عمر بن ابراهیم خیام نیشابوری
تولد: ۲۸ اردیبهشت ۴۲۷ خورشیدی، (۱۸ مه ۱۰۴۸ میلادی)، نیشابور
فوت: ۱۲ آذر ۵۱۰ خورشیدی، (۱۱۳۱ میلادی)، نیشابور
شهرت: ریاضیات، اخترشناسی، فلسفه، دین، تاریخ، گاهشماری، موسیقی
حکیم خیام نیشابوری
عمر خیام نیشابوری، که "خیامی" و "خیام نیشابوری" و "خیامی النیسابوری" هم نامیده شدهاست، فیلسوف، ریاضیدان، ستارهشناس و رباعی سرای ایرانی در دورهٔ سلجوقی است. گرچه پایگاه علمی خیام برتر از جایگاه ادبی او است و لقبش «حجةالحق» بودهاست؛ ولی آوازهٔ وی بیشتر به واسطهٔ نگارش رباعیاتش است که شهرت جهانی دارد. افزون بر آنکه رباعیات خیام را به اغلب زبانهای زنده ترجمه نمودهاند، ادوارد فیتزجرالد رباعیات او را به زبان انگلیسی ترجمه کردهاست که مایهٔ شهرت بیشتر وی در مغربزمین گردیدهاست.
یکی از برجستهترین کارهای وی را میتوان اصلاح گاهشماری ایران در زمان وزارت خواجه نظامالملک، که در دورهٔ سلطنت ملکشاه سلجوقی (۴۲۶ - ۴۹۰ هجری قمری) بود، دانست. وی در ریاضیات، علوم ادبی، دینی و تاریخی استاد بود. نقش خیام در حل معادلات درجه سوم و مطالعاتاش دربارهٔ اصل پنجم اقلیدس نام او را به عنوان ریاضیدانی برجسته در تاریخ علم ثبت کردهاست. ابداع نظریهای دربارهٔ نسبتهای همارز با نظریهٔ اقلیدس نیز از مهمترین کارهای اوست.
شماری از تذکرهنویسان، خیام را شاگرد ابن سینا و شماری نیز وی را شاگرد امام موفق نیشابوری خواندهاند. صحت این فرضیه که خیام شاگرد ابن سینا بودهاست، بسیار بعید مینماید، زیرا از لحاظ زمانی با هم تفاوت زیادی داشتهاند. خیام در جایی ابن سینا را استاد خود میداند اما این استادی ابن سینا، جنبهٔ معنوی دارد.
زندگی:
عمر خیام در سده پنجم هجری در نیشابور زاده شد. فقه را در میانسالی در محضر امام موفق نیشابوری آموخت؛ حدیث، تفسیر، فلسفه، حکمت و ستارهشناسی را فراگرفت. برخی نوشتهاند که او فلسفه را مستقیماً از زبان یونانی فرا گرفته بود.
در حدود ۴۴۹ تحت حمایت و سرپرستی ابوطاهر، قاضیالقضات سمرقند، کتابی دربارهٔ معادلههای درجهٔ سوم به زبان عربی نوشت تحت نام رساله فی البراهین علی مسائل الجبر و المقابله و از آنجاکه با نظامالملک طوسی رابطهای نیکو داشت، این کتاب را پس از نگارش به خواجه تقدیم کرد. پس از این دوران خیام به دعوت سلطان جلالالدین ملکشاه سلجوقی و وزیرش نظام الملک به اصفهان میرود تا سرپرستی رصدخانهٔ اصفهان را بهعهده گیرد. او هجده سال در آنجا مقیم میشود. به مدیریت او زیج ملکشاهی تهیه میشود و در همین سالها (حدود ۴۵۸) طرح اصلاح تقویم را تنظیم میکند. تقویم جلالی را تدوین کرد که به نام جلالالدین ملکشاه شهرهاست، اما پس از مرگ ملکشاه کاربستی نیافت. در این دوران خیام بهعنوان اختربین در دربار خدمت میکرد هرچند به اختربینی اعتقادی نداشت. در همین سالها (۴۵۶) مهمترین و تأثیرگذارترین اثر ریاضی خود را با نام رساله فی شرح مااشکل من مصادرات اقلیدس را مینویسد و در آن خطوط موازی و نظریهٔ نسبتها را شرح میدهد. همچنین گفته میشود که خیام هنگامی که سلطان سنجر، پسر ملکشاه در کودکی به آبله گرفتار بوده وی را درمان نمودهاست. پس از درگذشت ملکشاه و کشته شدن نظامالملک، خیام مورد بیمهری قرار گرفت و کمک مالی به رصدخانه قطع شد بعد از سال ۴۷۹ اصفهان را به قصد اقامت در مرو که به عنوان پایتخت جدید سلجوقیان انتخاب شده بود، ترک کرد. احتمالاً در آنجا میزان الحکم و قسطاس المستقیم را نوشت. رسالهٔ مشکلات الحساب (مسائلی در حساب) احتمالاً در همین سالها نوشته شدهاست. غلامحسین مراقبی گفتهاست که خیام در زندگی زن نگرفت و همسر برنگزید.
مرگ خیام را میان سالهای ۵۱۷-۵۲۰ هجری میدانند که در نیشابور اتفاق افتاد. گروهی از تذکرهنویسان نیز وفات او را ۵۱۶ نوشتهاند، اما پس از بررسیهای لازم مشخص گردیده که تاریخ وفات وی سال ۵۱۷ بودهاست .مقبرهٔ وی هم اکنون در شهر نیشابور، در باغی که آرامگاه امامزاده محروق در آن واقع میباشد، قرار گرفتهاست.
دستاوردهای خیام در ریاضیات:
س. ا. کانسوا گفته: «در تاریخ ریاضی سدههای ۱۱ و ۱۲ و شاید هم بتوان گفت در تمام سدههای میانه حکیم عمر خیام متولد نیشابور خراسان نقش عمدهای داشتهاست.»
پیش از کشف رساله خیام در جبر، شهرت او در مشرقزمین به واسطه اصلاحات سال و ماه ایرانی و در غرب به واسطه ترجمه رباعیاتش بودهاست. اگر چه کارهای خیام در ریاضیات (به ویژه در جبر) به صورت منبع دست اول در بین ریاضیدانان اروپایی سدهٔ ۱۹ میلادی مورد استفاده نبودهاست، میتوان رد پای خیام را به واسطه طوسی در پیشرفت ریاضیات در اروپا دنبال کرد. قدیمیترین کتابی که از خیام اسمی به میان آورده و نویسندهٔ آن همدوره خیام بوده، نظامی عروضی مؤلف «چهار مقاله» است. ولی او خیام را در ردیف منجمین ذکر میکند و اسمی از رباعیات او نمیآورد. با این وجود جورج سارتن با نام بردن از خیام به عنوان یکی از بزرگترین ریاضیدانان قرون وسطی چنین مینویسد:
خیام اول کسی است که به تحقیق منظم علمی در معادلات درجات اول و دوم و سوم پرداخته، و طبقهبندی تحسینآوری از این معادلات آوردهاست، و در حل تمام صور معادلات درجه سوم منظماً تحقیق کرده، و به حل (در اغلب موارد ناقص) هندسی آنها توفیق یافته، و رساله وی در علم جبر، که مشتمل بر این تحقیقات است، معرف یک فکر منظم علمی است؛ و این رساله یکی از برجستهترین آثار قرون وسطائی و احتمالاً برجستهترین آنها در این علم است. )غلامحسین مصاحب، ۱۳۵)
او نخستین کسی بود که نشان داد معادلهٔ درجهٔ سوم ممکن است دارای بیش از یک جواب باشد و یا این که اصلاً جوابی نداشته باشند.«آنچه که در هر حالت مفروض اتفاق میافتد بستگی به این دارد که مقاطع مخروطیای که وی از آنها استفاده میکند در هیچ نقطه یکدیگر را قطع نکنند، یا در یک یا دو نقطه یکدیگر را قطع کنند.». گفته اند: «نخستین کسی بود که گفت معادلهٔ درجهٔ سوم را نمیتوان عموماً با تبدیل به معادلههای درجهٔ دوم حل کرد، اما میتوان با بکار بردن مقاطع مخروطی به حل آن دست یافت.» همچنین «در مورد جبر، کار خیام در ابداع نظریهٔ هندسی معادلات درجهٔ سوم موفقترین کاری است که دانشمندی مسلمان انجام دادهاست.»
یکی دیگر از آثار ریاضی خیام رسالة فی شرح ما اشکل من مصادرات اقلیدس است. او در این کتاب اصل موضوعهٔ پنجم اقلیدس را دربارهٔ قضیهٔ خطوط متوازی که شالودهٔ هندسهٔ اقلیدسی است، مورد مطالعه قرار داد و اصل پنجم را اثبات کرد. به نظر میرسد که تنها نسخه کامل باقیمانده از این کتاب در کتابخانه لایدن در هلند قرار دارد. «در نیمهٔ اول سدهٔ هیجدهم، ساکری اساس نظریهٔ خود را دربارهٔ خطوط موازی بر مطالعهٔ همان چهارضلعی دوقائمهٔ متساویالساقین که خیام فرض کرده بود قرار میدهد و کوشش میکند که فرضهای حاده و منفرجهبودن دو زاویهٔ دیگر را رد کند.»
درکتاب دیگری از خیام که اهمیت ویژهای در تاریخ ریاضیات دارد رسالهٔ مشکلات الحساب (مسائلی در حساب) هرچند این رساله هرگز پیدا نشد اما خیام خود به این کتاب اشاره کردهاست و ادعا میکند قواعدی برای بسط دوجملهای کشف کرده و اثبات ادعایش به روش جبری در این کتاب است. بنابرین از دیگر دستآوردهای وی موفقیت در تعیین ضرایب بسط دو جملهای (بینوم نیوتن) است که البته تا سده قبل نامکشوف مانده بود و به احترام سبقت وی بر اسحاق نیوتن در این زمینه در بسیاری از کتب دانشگاهی و مرجع این دو جملهایها «دو جملهای خیام-نیوتن» نامیده میشوند. نوشتن این ضرایب به صورت منظم مثلث خیام-پاسکال را شکل میدهد که بیانگر رابطه ای بین این ضرایب است.
درکتاب دیگری از خیام که اهمیت ویژهای در تاریخ ریاضیات دارد رسالهٔ مشکلات الحساب (مسائلی در حساب) هرچند این رساله هرگز پیدا نشد اما خیام خود به این کتاب اشاره کرده است و ادعا میکند قواعدی برای بسط دوجملهای (a + b)n کشف کرده و اثبات ادعایش به روش جبری در این کتاب است.
به هر حال قواعد این بسط تا n = 12 توسط طوسی (که بیشترین تاثیر را از خیام گرفته) در کتاب «جوامع الحساب» آورده شده است.
روش خیام در به دست آوردن ضرایب منجر به نام گذاری مثلث حسابی این ضرایب به نام مثلث خیام شد، انگلیسی زبانها آن را به نام مثلث پاسکال میشناسند که البته خدشهای بر پیشگامی خیام در کشف روشی جبری برای این ضرایب نیست.
خیام به تحلیل ریاضی موسیقی نیز پرداخته است و در القول علی اجناس التی بالاربعاء مسالهٔ تقسیم یک چهارم را به سه فاصله مربوط به مایههای بینیمپرده، با نیمپردهٔ بالارونده، و یک چهارم پرده را شرح میدهد.
مثلث خیام ـ پاسكال یكی از زیباترین نگارههای عددی است كه در تاریخ ریاضیات مورد توجه ریاضیدانان قرار گرفته است.

مثلث خیام - پاسکال
به سهولت مشخص میشود كه هر سطر با سطر بالاتر از خود چه رابطهای دارد.
یكی از خواص این مثلث آن است كه مجموع اعداد هر سطر برابر است با توانهای از صفر تا n عدد 2. حال به بسط دوجملهای خیام ـ نیوتن توجه كنیم:
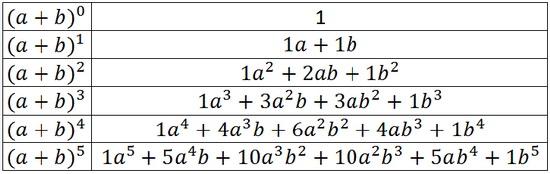
بسط دو جمله ای با استفاده از اعداد مثلث خیام - پاسکال
اگر به ضرایب بسط دو جملهای توجه شود، همان اعداد مثلث فوقالذكر هستند. یا به عبارتی اگر به جای a و b عدد 1 گذاشته شود، این بسط، همان مثلث خیام - پاسکال را تشكیل میدهد.
مأخذ: دانشنامهٔ آزاد ویکی پدیا (با تکمیل مطلب)