نظریهی پیچیدگی محاسباتی شاخهای از علوم کامپیوتر و ریاضی است که به بررسی دشواری حل مسائل به وسیلهی رایانه (به عبارت دقیقتر به صورت الگوریتمی) میپردازد. این نظری بخشی از نظریهی محاسباتی است که با منابع مورد نیاز برای حل یک مساله سروکار دارد. عمومیترین منابع زمان (چقدر زمان برای حل کردن مساله لازم است) و فضا (چقدر حافظه مورد نیاز است) میباشند. سایر منابع میتواند تعداد پروسسورهای موازی (در حالت پردازش موازی) و … باشند. اما در این مقاله ما در مورد عواملی مثل عوامل بالا بحثی نکردهایم.
باید به این نکته توجه داشت که نظریه پیچیدگی با نظریه قابل حل بودن متفاوت میباشد. این نظریه در مورد قابل حل بودن یک مساله بدون توجه به منابع مورد نیاز آن، بحث میکند. بعد از این نظریه که بیان میکند کدام مسائل قابل حل میباشند و کدام مسائل غیرقابل حل، این سوال به نظر طبیعی میرسد که درجه سختی مساله چقدر است. نظریه پیچیدگی محاسبات در این زمینه میباشد.
برای سادگی کار مسالهها به کلاسهایی تقسیم میشوند به طوری که مسالههای یک کلاس از حیث زمان یا فضای مورد نیاز با هم مشابهت دارند. این کلاسها در اصطلاح کلاسهای پیچیدگی خوانده میشوند.
بعضی منابع دیگری که در این نظریه مورد بررسی قرار میگیرند، مثل عدم تعیین صرفا جنبهی صوری دارند ولی بررسی آنها موجب درک عمیقتر منابع واقعی مثل زمان و فضا میشود.
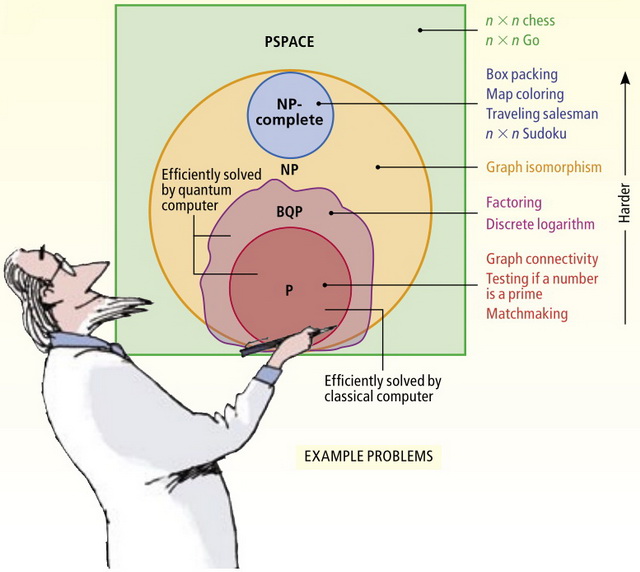
معروفترین کلاسهای پیچیدگی، P و NP هستند که مسالهها را از نظر زمان مورد نیاز تقسیمبندی میکنند. به طور شهودی میتوان گفت P کلاس مسالههایی است که الگوریتمهای سریع برای پیدا کردن جواب آنها وجود دارد. اما NP شامل آن دسته از مسالههاست که اگرچه ممکن است پیدا کردن جواب برای آنها نیاز به زمان زیادی داشته باشد اما چک کردن درستی جواب به وسیلهٔ یک الگوریتم سریع ممکن است. البته کلاسهای پیچیدگی به مرتبه سختتری از NP نیز وجود دارند.
▪ PSPACE: مسائلی که با اختصاص دادن مقدار کافی حافظه (که این مقدار حافظه معمولا تابعی از اندازه مساله میباشد) بدون در نظر گرفتن زمان مورد نیاز به حل آن، میتوانند حل شوند.
▪ EXPTIME: مسائلی که زمان مورد نیاز برای حل آنها به صورت توانی میباشد. مسائل این کلاس بسیار جذاب و سرگرم کننده میباشند (حداقل برای ما!). و شامل همه مسائل سه کلاس بالایی نیز میباشد. نکته جالب و قابل توجه این میباشد که حتی این کلاس نیز جامع نمیباشد. یعنی مسائلی وجود دارند که بهترین و کارامدترین الگوریتمها نیز زمان بیشتری نسبت به زمان توانی میگیرند.
▪ Un-decidable یا غیرقابل تصمیمگیری: برای برخی از مسائل میتوانیم اثبات کنیم که الگوریتمی را نمیشود پیدا کردن که همیشه آن مساله را حل میکند، بدون در نظر گرفتن فضا و زمان. در این زمینه آقای ریچارد لیپتون (از صاحبنظران این زمینه) در مقالهای نوشتهاند: یک روش اثبات غیررسمی برای این مساله میتواند این باشد: تعداد زیادی مساله، مثلا به زیادی اعداد حقیقی وجود دارند، ولی تعداد برنامههایی که مسائل را حل میکنند در حد اعداد صحیح میباشند. اما ما همیشه میتوانیم مسائل به دردبخوری را پیدا کنیم که قابل حل نمیباشند.
● آیا P=NP میباشد؟
این سوال که آیا مسائل کلاس P دقیقا همان مسائل کلاس NP می باشند، یکی از مهم ترین سوالهای بدون جواب علوم کامپیوتری میباشد. به بیانی دیگر اگر همیشه به این سادگی باشد که بتوان صحت یک راهحل را بررسی کرد، آیا پیدا کردن راهحل نیز میتواند به آن سادگی باشد؟ برای این سوال یک جایزه ۱ میلیون دلاری از طرف انسیتیتو ریاضی Clay در نظرگرفته شدهاست. ما هیچ دلیلی برای قبول کردن آن نداریم ولی بین نظریهپردازان نیز این باور وجود دارد که باید جواب این سوال منفی باشد. همچنین دلیلی برای رد کردن آن نیز وجود ندارد.
● پیچیدگی زمانی
پیچیدگی زمانی یک مساله تعداد گامهای مورد نیاز برای حل یک نمونه از یک مساله به عنوان تابعی از اندازهی ورودی (معمولا بوسیله تعداد بیتها بیان میشود) بوسیله کارآمدترین الگوریتم میباشد. برای درک بهتر این مساله، فرض کنید که یک مساله با ورودی n بیت در n² گام حل شود. در این مثال میگوییم که مساله از درجه پیچیدگی n² میباشد. البته تعداد دقیق گامها بستگی به ماشین و زبان مورد استفاده دارد. اما برای صرف نظر کردن از این مشکل، نشانهگذاری O بزرگ (Big O notation) معمولا بکار میرود. اگر یک مساله پیچیدگی زمانی از مرتبه (O(n² روی یک کامپیوتر نمونه داشته باشد، معمولا روی اکثر کامپیوترهای دیگر نیز پیچیدگی زمانی از مرتبه (O(n² خواهد داشت. پس این نشانه به ما کمک میکند که صرف نظر از یک کامپیوتر خاص، یک حالت کلی برای پیچیدگی زمانی یک الگوریتم ارائه دهیم.
● معرفی NP-Complete
تا این بخش از مقاله مسائلی معرفی شدند که اگر بتوان روشی برای حل آنها حدس زد، در زمان نزدیک به زمان خطی و یا حداقل در زمان چند جملهای برحسب ورودی میتوانستیم صحت راهحل را بررسی کنیم. ولی NP-Completeها مسائلی هستند که اثبات شده به سرعت قابل حل نیستند. در تئوری پیچیدگی NP-Completeها دشوارترین مسائل کلاس NP هستند و جزء مسائلی میباشند که احتمال حضورشان در کلاس P خیلی کم است. علت این امر این میباشد که اگر یک راهحل پیدا شود که بتواندیک مساله NP-Complete را حل کند، میتوان از آن الگوریتم برای حل کردن سریع همه مسائل NP-Complete استفاده کرد. به خاطر این مساله و نیز بخاطر اینکه تحقیقات زیادی برای پیدا کردن الگوریتم کارآمدی برای حل کردن اینگونه مسائل با شکست مواجه شدهاند، وقتی که مسالهای به عنوان NP-Complete معرفی شد، معمولا اینطور قلمداد میشود که این مساله در زمان Polynomial قابل حل شدن نمیباشد، یا به بیانی دیگر هیچ الگوریتمی وجود ندارد که این مساله را در زمان Polynomial حل نماید. کلاس متشکل از مسائل NP-Compete با نام NP-C نیز خوانده میشود.
● بررسی ناکارآمد بودن زمانی
مسائلی که در تئوری قابل حل شدن میباشند ولی در عمل نمیتوان آنها را حل کرد، محال یا ناشدنی مینامند. در حالت کلی فقط مسائلی که زمان آنها به صورت Polynomial میباشد و اندازه ورودی آنها در حد کوچک یا متوسط میباشد قابل حل شدن میباشند. مسائلی که زمان آنها به صورت توانی (EXPTIME-Complete) میباشند به عنوان مسائل محال یا ناشدنی شناخته شدهاند. همچنین اگر مسائل رده NP جز مسائل رده P نباشند، مسائل NP-Complete نیز به عنوان محال یا نشدنی خواهند بود. برای ملموستر شدن این مساله فرض کنید که یک مساله ۲n مرحله لازم دارد تا حل شود (n اندازه ورودی میباشد). برای مقادیر کوچک n=۱۰۰ و با در نظر گرفتن کامپیوتری که ۱۰۱۰ (۱۰ giga) عملیات را در یک ثانیه انجام میدهد، حل کردن این مساله زمانی حدود ۱۰۱۲ * ۴ سال طول خواهد کشید، که این زمان از عمر فعلی جهان بیشتر است!
● چرا حل مسائل NP-Complete مشکل است؟
به خاطر اینکه مسائل بسیار مهمی در این کلاس وجود دارد، تلاشهای بسیار زیادی صورت گرفته است تا الگوریتمهایی برای حل مسائل NP که زمان آن به صورت Polynomial از اندازه ورودی باشد، پیدا شود. باوجود این، مسائل خیلی بیشتری در این رده وجود دارد که زمان لازم برای حل آنها به صورت Super-Polynomial میباشد. این مساله که آیا این مسائل در زمان Polynomial قابل حل شدن میباشند، یکی از مهمترین چالشهای علوم کامپیوتری میباشد.
● روشهایی برای حل مسائل NP-Complete
به خاطر اینکه تعداد مسائل NP-Complete بسیار زیاد میباشد، شناختن اینگونه مسائل به ما کمک میکند تا دست از پیدا کردن یک الگوریتم سریع و جامع برداریم و یکی از روشهای زیر را امتحان کنیم:
▪به کار بردن یک روش حدسی: یک الگوریتم که تا حد قابل قبولی در بیشتر موارد درست کار میکند، ولی تضمینی وجود ندارد که در همه موارد با سرعت قابل قبول نتیجه درستی تولید کند.
▪ حل کردن تقریبی مساله به جای حل کردن دقیق آن: اغلب موارد این روش قابل قبول میباشد که با یک الگوریتم نسبتا سریع یک مساله را به طور تقریبی حل کنیم که میتوان ثابت کرد جواب بدست آمده تقرییا نزدیک به جواب کاملا صحیح میباشد.
▪ الگوریتمهای زمان توانی را به کار ببریم: اگر واقعا مجبور به حل کردن مساله به طور کامل هستیم، میتوان یک الگوریتم با زمان توانی نوشت و دیگر نگران پیدا کردن جواب بهتر نباشیم.
▪ از خلاصه کردن استفاده کنیم: خلاصه کردن به این مفهوم میباشد که از برخی اطلاعات غیرضروری میتوان صرف نظر کرد. اغلب این اطلاعات برای پیادهسازی مساله پیچیده در دنیای واقعی مورد نیاز میباشد، ولی در شرایطی که بخواهیم به نحوی مساله را حل کنیم (حداقل به صورت تئوری و نه در عمل) میتوان از برخی اطلاعات غیرضروری صرف نظر کرد.
● نمونه مساله
یک مسیر ساده در یک گراف به مسیری اطلاق میشود که هیچ راس یا یال تکراری در آن وجود نداشتهباشد. برای پیاده سازی مساله ما به این احتیاج داریم که بتوانیم یک سوال بلی/خیر طراحی کنیم. با داشتن گراف G، رئوس s و t و عدد k آیا یک مسیر ساده از s به t با حداقل k یال وجود دارد؟
راهحل این مساله جواب سوال خواهد بود. چرا این مساله NP میباشد؟ چون اگر مسیری به شما داده شود، به راحتی میتوان طول مسیر را مشخص نمود و آن را با k مقایسه کرد. همه این کارها در زمان خطی و صد البته در زمان Polynomial قابل انجام میباشد. اگر چه می نمیدانیم که این مساله آیا در کلاس P میباشد یا نه، با این حال روش خاصی برای پیدا کردن مسیری با ویژگیهای ذکر شده نیز وجود بیان نشده است. و در حقیقت این مساله جز NP-Completeها میباشد، پس میتوان به این نتیجه نیز رسید که الگوریتمی کارآمد با چنان عملیات وجود ندارد. الگوریتمهایی وجود دارند که این مساله را حل میکنند، به عنوان مثال همه مسیرهای موجود و ممکن را بررسی نموده و نتایج مقایسه شوند که آیا این مسیر مساله را حل میکند یا نه. اما تا آنجایی که میدانیم، الگوریتمی با زمان Polynomial برای حل این مساله وجود ندارد.